Elliptic integrals
Despite the "unreasonable effectiveness"1 of mathematics applied to physics, I think it is important to remember that there is an awful lot we cannot calculate exactly. In general, except for the simplest of problems, numerical computations or some other type of approximation are the only way to get answers.
I find the elliptic integrals a fascinating illustration of this reality. These are a particular class of the so-called "special functions"—the relatively obscure2 functions which typically arise as solutions to differential equations and which do not have a closed-form expression.
Two types of elliptic integrals which I have spent some time studying recently are the elliptic integral of the first kind,
\[\textrm{F}(\phi ;\ \alpha) = \int_0^\phi \frac{\textrm{d}\theta}{\sqrt{1-\sin^2 \alpha \sin^2 \theta}}.\]
and the elliptic integral of the second kind,
\[\textrm{E}(\phi ;\ \alpha) = \int_0^\phi \textrm{d}\theta\ \sqrt{1-\sin^2 \alpha \sin^2 \theta}.\]
For the parameter \(\phi = \frac{\pi}{2}\) these integrals are said to be complete and one convention I have seen is to denote the complete elliptic integral of the first kind as \(\textrm{K}(\alpha)\). Since \(\alpha\) is an arbitrary parameter, sometimes the integrals are written with \(m = \sin^2 \alpha\) instead. In the plot below, yet another convention is used, \(k = \sin \alpha\).
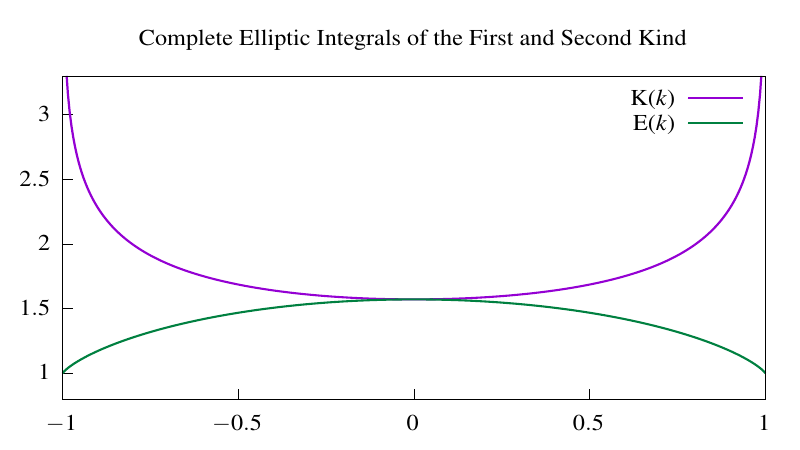
As an example of where these integrals come up (and an explanation for the name), consider the arc length of an arbitrary ellipse. In Cartesian coordinates, the equation is:
\[\frac{x^2}{a^2} + \frac{y^2}{b^2} = 1.\]
From differential geometry, the general formula for the arc length of a "nice enough" parametric curve \(\gamma(t)\) from 0 to \(t\) is \(s(t) = \int_0^t \textrm{d}\tilde{t}\ \lVert \gamma(\tilde{t}) \rVert\). Using a standard parameterization in polar coordinates, this formula in the case of an ellipse becomes,
\[s(t) = \int_0^\phi \textrm{d}\theta\ \sqrt{a^2 \cos^2{\theta} + b^2 \sin^2 \theta}.\]
After writing \(\cos^2 \theta = 1-\sin^2\theta\) and pulling \(a^2\) from under the radical,
\[s(t) = a \int_0^\phi \textrm{d}\theta\ \sqrt{1 + \frac{b^2 - a^2}{a^2} \sin^2 \theta} = a \int_0^\phi \textrm{d}\theta\ \sqrt{1 - \frac{a^2 - b^2}{a^2} \sin^2 \theta}.\]
Setting \(m = \frac{a^2 - b^2}{a^2}\), and this is the proper form of the incomplete elliptic integral of the second kind. To compute the arc length in the first quadrant, we have \(\phi = \frac{\pi}{2}\), hence
\[s = a \textrm{K}\left(\frac{a^2 - b^2}{a^2}\right).\]
Because there is no closed form for this integral, the value must be computed numerically. Back in the day, engineers and physicists would refer to massive volumes of tabulated data for this purpose. These days, anyone can look it up with a CAS. For example, the evaluation with maxima for the ellipse with semi-major axis 4 and semi-minor axis 2 units can be calculated with float(4*elliptic_ec((16-4)/16));, which gives the approximate answer 4.844 units.
To go out on a limb, I suspect the exact expressions of elliptic integrals are less important now that nobody needs to look them up in a table anymore. Numerical integration programs are a dime a dozen these days, so you do not really need to massage integrands into certain forms anymore to compute the answer. Still, I find the techniques interesting.
A harder example is related to the magnetic vector potential of a circular current loop in the plane. It was actually from trying to calculate this while studying for my electricity and magnetism course this past semester that I realized just how ubiquitous the elliptic integrals are! The integral is already quite an exercise to set up, but in cylindrical coordinates we have,
\[ A_{\phi}(\vec{r}) = \frac{a \mu_{0} I}{4\pi} \int_{0}^{2\pi} \textrm{d}\phi' \frac{\cos \phi'}{\sqrt{\rho^{2} + a^{2} + z^2 - 2a \rho \cos \phi'}}.\]
Where a is the loop radius, \(\vec{r} = \rho \hat{e}_{\rho} + z \hat{e}_{z}\) is the point of interest and primed coordinates are the source points; \(\phi' \in [0,2\pi]\).
This can be transformed into,
\[\frac{\mu_{0} I}{\pi} \sqrt{\frac{a}{\rho}} \left(\left(1-\frac{m}{2}\right)\textrm{K}(m) - \textrm{E}(m) \right).\]
Where \(m = \frac{4a \rho}{(\rho + a)^{2} + z^{2}}\).
The derivation is best described as a pain in the ass, as quite a few non-obvious substitutions are used:
- Let \(\cos \phi' = 2\cos^{2} \frac{\phi'}{2} - 1\) in the denominator.
- Substitute \(\frac{\phi'}{2} = u + \frac{\pi}{2}\) so that \(\textrm{d}\phi' = 2\textrm{d}u\). (This changes the integral limits to be \(-\frac{\pi}{2} to \frac{\pi}{2}\).)
- After the above substitution, \(\cos^{2} \frac{\phi'}{2} = \sin^2 u\).
- \(\cos(2u + \pi) = -(1-2\sin^{2} u)\).
- And finally, the following identity of elliptic integrals is useful.
\[\int_0^\phi \textrm{d}\theta \frac{\sin^{2} \theta}{\sqrt{1-m\sin^{2}\theta}} = \frac{1}{m} \left(\textrm{F}(\phi ;\ m) - \textrm{E}(\phi ;\ m)\right).\]
Phew. All this is interesting mathematics if you like lengthy calculations, but there is not much physics going on. An alternative method, which trades the "exact" expression for more information on what the field quantity looks like, is the multipole expansion. This technique obtains approximate expressions for potentials by expanding their integrands in a power series of Legendre polynomials. Not only is this method more tractable, but it makes it easier to visualize what happens nearby and far away from the source by seeing which terms dominate the expansion.
In terms of further reading, I would suggest Mathematical Methods for Physicists by Arfken and Advanced Engineering Mathematics by Kreyszig (the latter specifically for Legendre polynomials). There are also some more online references here, here and here.
1: C.f. "The Unreasonable Effectiveness of Mathematics in the Natural Sciences" by Wigner (opens a pdf)
2: Well, obscure to the average Calc I student, but not to the average electrical engineer.